Recommender Systems
Collaborative Filtering based Recommender System
DataSet: Click here
Link to Databricks Notebook: Click here
Summary
Trained an Alternating Least Squares (ALS – WR) model for Collaborative filtering on the movielens data and evaluated the model on the validation data by measuring the Root Mean Squared Error and used the best model to recommend 25 movies with highest predicted ratings
Part 0: Preliminaries
We read in each of the files and create an RDD consisting of parsed lines.
Each line in the ratings dataset (ratings.dat.gz) is formatted as:
UserID::MovieID::Rating::Timestamp
Each line in the movies (movies.dat) dataset is formatted as:
MovieID::Title::Genres
The Genres field has the format
Genres1|Genres2|Genres3|...
The format of these files is uniform and simple, so we can use Python split() to parse their lines.
Parsing the two files yields two RDDS
- For each line in the ratings dataset, we create a tuple of (UserID, MovieID, Rating). We drop the timestamp because we do not need it for this exercise.
- For each line in the movies dataset, we create a tuple of (MovieID, Title). We drop the Genres because we do not need them for this exercise.
Part 1: Basic Recommendations
One way to recommend movies is to always recommend the movies with the highest average rating. In this part, we will use Spark to find the name, number of ratings, and the average rating of the 20 movies with the highest average rating and more than 500 reviews. We want to filter our movies with high ratings but fewer than or equal to 500 reviews because movies with few reviews may not have broad appeal to everyone.
(1a) Number of Ratings and Average Ratings for a Movie
Using only Python, implement a helper function getCountsAndAverages() that takes a single tuple of (MovieID, (Rating1, Rating2, Rating3, …)) and returns a tuple of (MovieID, (number of ratings, averageRating)). For example, given the tuple (100, (10.0, 20.0, 30.0)), your function should return (100, (3, 20.0))
First, implement a helper function getCountsAndAverages using only Python
def getCountsAndAverages(IDandRatingsTuple):
""" Calculate average rating
Args:
IDandRatingsTuple: a single tuple of (MovieID, (Rating1, Rating2, Rating3, ...))
Returns:
tuple: a tuple of (MovieID, (number of ratings, averageRating))
"""
MovieID = IDandRatingsTuple[0]
numRatings = len(IDandRatingsTuple[1])
avgRatings = float(sum(IDandRatingsTuple[1])) / numRatings
return (MovieID, (numRatings, avgRatings))
(1b) Movies with Highest Average Ratings
Now that we have a way to calculate the average ratings, we will use the getCountsAndAverages() helper function with Spark to determine movies with highest average ratings.
The steps you should perform are:
- Recall that the
ratingsRDDcontains tuples of the form (UserID, MovieID, Rating). FromratingsRDDcreate an RDD with tuples of the form (MovieID, Python iterable of Ratings for that MovieID). This transformation will yield an RDD of the form:[(1, <pyspark.resultiterable.ResultIterable object at 0x7f16d50e7c90>), (2, <pyspark.resultiterable.ResultIterable object at 0x7f16d50e79d0>), (3, <pyspark.resultiterable.ResultIterable object at 0x7f16d50e7610>)]. Note that you will only need to perform two Spark transformations to do this step. - Using
movieIDsWithRatingsRDDand yourgetCountsAndAverages()helper function, compute the number of ratings and average rating for each movie to yield tuples of the form (MovieID, (number of ratings, average rating)). This transformation will yield an RDD of the form:[(1, (993, 4.145015105740181)), (2, (332, 3.174698795180723)), (3, (299, 3.0468227424749164))]. You can do this step with one Spark transformation - We want to see movie names, instead of movie IDs. To
moviesRDD, apply RDD transformations that usemovieIDsWithAvgRatingsRDDto get the movie names formovieIDsWithAvgRatingsRDD, yielding tuples of the form (average rating, movie name, number of ratings). This set of transformations will yield an RDD of the form:[(1.0, u'Autopsy (Macchie Solari) (1975)', 1), (1.0, u'Better Living (1998)', 1), (1.0, u'Big Squeeze, The (1996)', 3)]. You will need to do two Spark transformations to complete this step: first use themoviesRDDwithmovieIDsWithAvgRatingsRDDto create a new RDD with Movie names matched to Movie IDs, then convert that RDD into the form of (average rating, movie name, number of ratings). These transformations will yield an RDD that looks like:[(3.6818181818181817, u'Happiest Millionaire, The (1967)', 22), (3.0468227424749164, u'Grumpier Old Men (1995)', 299), (2.882978723404255, u'Hocus Pocus (1993)', 94)]
(1c) Movies with Highest Average Ratings and more than 500 reviews
Now that we have an RDD of the movies with highest averge ratings, we can use Spark to determine the 20 movies with highest average ratings and more than 500 reviews.
Apply a single RDD transformation to movieNameWithAvgRatingsRDD to limit the results to movies with ratings from more than 500 people. We then use the sortFunction() helper function to sort by the average rating to get the movies in order of their rating (highest rating first). You will end up with an RDD of the form:
[(4.5349264705882355, u'Shawshank Redemption, The (1994)', 1088), (4.515798462852263, u"Schindler's List (1993)", 1171), (4.512893982808023, u'Godfather, The (1972)', 1047)]
Part 2: Collaborative Filtering
In this course, you have learned about many of the basic transformations and actions that Spark allows us to apply to distributed datasets. Spark also exposes some higher level functionality; in particular, Machine Learning using a component of Spark called MLlib. In this part, you will learn how to use MLlib to make personalized movie recommendations using the movie data we have been analyzing.
We are going to use a technique called collaborative filtering. Collaborative filtering is a method of making automatic predictions (filtering) about the interests of a user by collecting preferences or taste information from many users (collaborating). The underlying assumption of the collaborative filtering approach is that if a person A has the same opinion as a person B on an issue, A is more likely to have B’s opinion on a different issue x than to have the opinion on x of a person chosen randomly. You can read more about collaborative filtering here.
The image below (from Wikipedia) shows an example of predicting of the user’s rating using collaborative filtering. At first, people rate different items (like videos, images, games). After that, the system is making predictions about a user’s rating for an item, which the user has not rated yet. These predictions are built upon the existing ratings of other users, who have similar ratings with the active user. For instance, in the image below the system has made a prediction, that the active user will not like the video.

%md For movie recommendations, we start with a matrix whose entries are movie ratings by users (shown in red in the diagram below). Each column represents a user (shown in green) and each row represents a particular movie (shown in blue).
Since not all users have rated all movies, we do not know all of the entries in this matrix, which is precisely why we need collaborative filtering. For each user, we have ratings for only a subset of the movies. With collaborative filtering, the idea is to approximate the ratings matrix by factorizing it as the product of two matrices: one that describes properties of each user (shown in green), and one that describes properties of each movie (shown in blue).
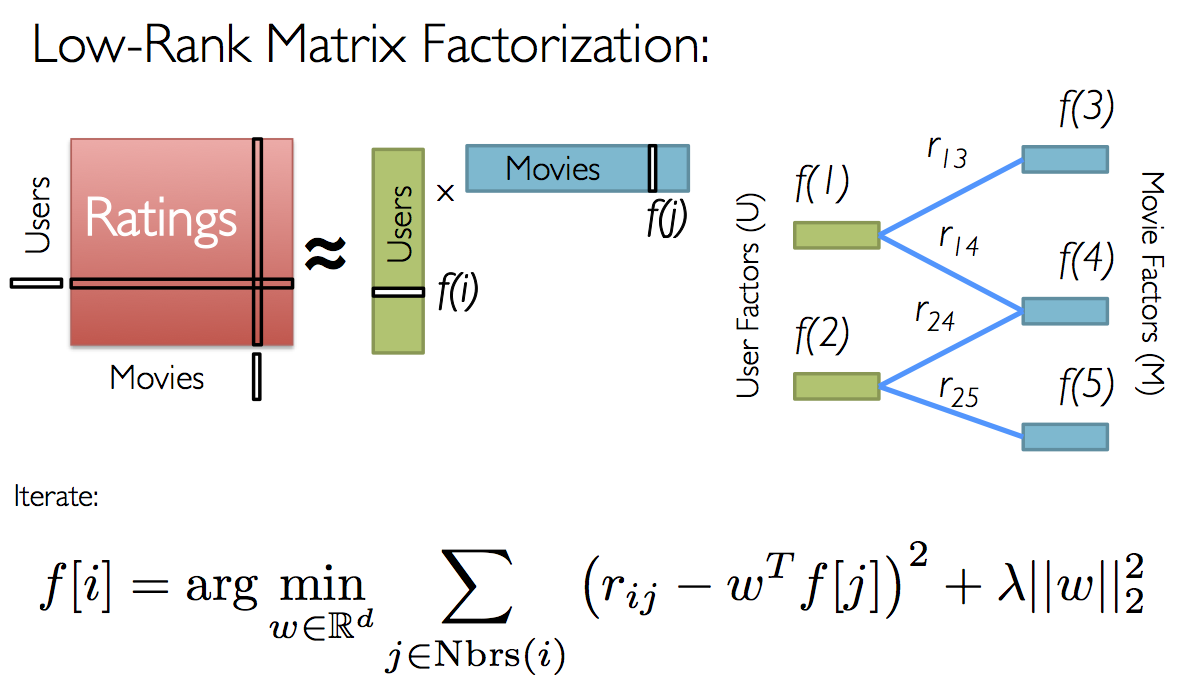 We want to select these two matrices such that the error for the users/movie pairs where we know the correct ratings is minimized. The [Alternating Least Squares][als] algorithm does this by first randomly filling the users matrix with values and then optimizing the value of the movies such that the error is minimized. Then, it holds the movies matrix constrant and optimizes the value of the user’s matrix. This alternation between which matrix to optimize is the reason for the “alternating” in the name.
We want to select these two matrices such that the error for the users/movie pairs where we know the correct ratings is minimized. The [Alternating Least Squares][als] algorithm does this by first randomly filling the users matrix with values and then optimizing the value of the movies such that the error is minimized. Then, it holds the movies matrix constrant and optimizes the value of the user’s matrix. This alternation between which matrix to optimize is the reason for the “alternating” in the name.
This optimization is what’s being shown on the right in the image above. Given a fixed set of user factors (i.e., values in the users matrix), we use the known ratings to find the best values for the movie factors using the optimization written at the bottom of the figure. Then we “alternate” and pick the best user factors given fixed movie factors.
For a simple example of what the users and movies matrices might look like, check out the [videos from Lecture 8][videos] or the [slides from Lecture 8][slides] [videos]: https://courses.edx.org/courses/BerkeleyX/CS100.1x/1T2015/courseware/00eb8b17939b4889a41a6d8d2f35db83/3bd3bba368be4102b40780550d3d8da6/ [slides]: https://courses.edx.org/c4x/BerkeleyX/CS100.1x/asset/Week4Lec8.pdf [als]: https://en.wikiversity.org/wiki/Least-Squares_Method
(2a) Creating a Training Set
Before we jump into using machine learning, we need to break up the ratingsRDD dataset into three pieces:
- A training set (RDD), which we will use to train models
- A validation set (RDD), which we will use to choose the best model
- A test set (RDD), which we will use for our experiments
To randomly split the dataset into the multiple groups, we can use the pySpark randomSplit() transformation.
randomSplit()takes a set of splits and and seed and returns multiple RDDs.
After splitting the dataset, your training set has about 293,000 entries and the validation and test sets each have about 97,000 entries (the exact number of entries in each dataset varies slightly due to the random nature of the randomSplit() transformation.
(2b) Root Mean Square Error (RMSE)
In the next part, you will generate a few different models, and will need a way to decide which model is best. We will use the Root Mean Square Error (RMSE) or Root Mean Square Deviation (RMSD) to compute the error of each model. RMSE is a frequently used measure of the differences between values (sample and population values) predicted by a model or an estimator and the values actually observed. The RMSD represents the sample standard deviation of the differences between predicted values and observed values. These individual differences are called residuals when the calculations are performed over the data sample that was used for estimation, and are called prediction errors when computed out-of-sample. The RMSE serves to aggregate the magnitudes of the errors in predictions for various times into a single measure of predictive power. RMSE is a good measure of accuracy, but only to compare forecasting errors of different models for a particular variable and not between variables, as it is scale-dependent.
The RMSE is the square root of the average value of the square of (actual rating - predicted rating) for all users and movies for which we have the actual rating. Versions of Spark MLlib beginning with Spark 1.4 include a RegressionMetrics module that can be used to compute the RMSE. However, since we are using Spark 1.3.1, we will write our own function.
Write a function to compute the sum of squared error given predictedRDD and actualRDD RDDs. Both RDDs consist of tuples of the form (UserID, MovieID, Rating)
To calculate RSME, the steps you should perform are:
- Transform
predictedRDDinto the tuples of the form ((UserID, MovieID), Rating). For example, tuples like[((1, 1), 5), ((1, 2), 3), ((1, 3), 4), ((2, 1), 3), ((2, 2), 2), ((2, 3), 4)]. You can perform this step with a single Spark transformation. - Transform
actualRDDinto the tuples of the form ((UserID, MovieID), Rating). For example, tuples like[((1, 2), 3), ((1, 3), 5), ((2, 1), 5), ((2, 2), 1)]. You can perform this step with a single Spark transformation. - Using only RDD transformations (you only need to perform two transformations), compute the squared error for each matching entry (i.e., the same (UserID, MovieID) in each RDD) in the reformatted RDDs - do not use
collect()to perform this step. Note that not every (UserID, MovieID) pair will appear in both RDDs - if a pair does not appear in both RDDs, then it does not contribute to the RMSE. You might want to check out Python’s math module to see how to compute these values - Using an RDD action (but not
collect()), compute the total squared error - Compute n by using an RDD action (but not
collect()), to count the number of pairs for which you computed the total squared error - Using the total squared error and the number of pairs, compute the RSME. Make sure you compute this value as a float.
Note: Your solution must only use transformations and actions on RDDs. Do not call collect() on either RDD.
import math
def computeError(predictedRDD, actualRDD):
""" Compute the root mean squared error between predicted and actual
Args:
predictedRDD: predicted ratings for each movie and each user where each entry is in the form
(UserID, MovieID, Rating)
actualRDD: actual ratings where each entry is in the form (UserID, MovieID, Rating)
Returns:
RSME (float): computed RSME value
"""
# Transform predictedRDD into the tuples of the form ((UserID, MovieID), Rating)
predictedReformattedRDD = predictedRDD.map(lambda x: ((x[0], x[1]), x[2]))
# Transform actualRDD into the tuples of the form ((UserID, MovieID), Rating)
actualReformattedRDD = actualRDD.map(lambda x: ((x[0], x[1]), x[2]))
# Compute the squared error for each matching entry (i.e., the same (User ID, Movie ID) in each
# RDD) in the reformatted RDDs using RDD transformtions - do not use collect()
squaredErrorsRDD = (predictedReformattedRDD
.join(actualReformattedRDD).map(lambda x: (x[1][1] - x[1][0])**2))
# Compute the total squared error - do not use collect()
totalError = squaredErrorsRDD.reduce(lambda x, y: x + y)
# Count the number of entries for which you computed the total squared error
numRatings = squaredErrorsRDD.count()
# Using the total squared error and the number of entries, compute the RSME
return math.sqrt(float(totalError) / numRatings)
(2c) Using ALS.train()
In this part, we will use the MLlib implementation of Alternating Least Squares, ALS.train(). ALS takes a training dataset (RDD) and several parameters that control the model creation process. To determine the best values for the parameters, we will use ALS to train several models, and then we will select the best model and use the parameters from that model in the rest of this lab exercise.
The process we will use for determining the best model is as follows:
- Pick a set of model parameters. The most important parameter to
ALS.train()is the rank, which is the number of rows in the Users matrix (green in the diagram above) or the number of columns in the Movies matrix (blue in the diagram above). (In general, a lower rank will mean higher error on the training dataset, but a high rank may lead to overfitting.) We will train models with ranks of 4, 8, and 12 using thetrainingRDDdataset. - Create a model using
ALS.train(trainingRDD, rank, seed=seed, iterations=iterations, lambda_=regularizationParameter)with three parameters: an RDD consisting of tuples of the form (UserID, MovieID, rating) used to train the model, an integer rank (4, 8, or 12), a number of iterations to execute (we will use 5 for theiterationsparameter), and a regularization coefficient (we will use 0.1 for theregularizationParameter). - For the prediction step, create an input RDD,
validationForPredictRDD, consisting of (UserID, MovieID) pairs that you extract fromvalidationRDD. You will end up with an RDD of the form:[(1, 1287), (1, 594), (1, 1270)] - Using the model and
validationForPredictRDD, we can predict rating values by calling model.predictAll() with thevalidationForPredictRDDdataset, wheremodelis the model we generated with ALS.train().predictAllaccepts an RDD with each entry in the format (userID, movieID) and outputs an RDD with each entry in the format (userID, movieID, rating). - Evaluate the quality of the model by using the
computeError()function you wrote in part (2b) to compute the error between the predicted ratings and the actual ratings invalidationRDD.
Which rank produces the best model, based on the RMSE with the validationRDD dataset?
Note: It is likely that this operation will take a noticeable amount of time (around a minute in our VM); you can observe its progress on the Spark Web UI. Probably most of the time will be spent running your
computeError()function, since, unlike the Spark ALS implementation (and the Spark 1.4 RegressionMetrics module), this does not use a fast linear algebra library and needs to run some Python code for all 100k entries.
(2d) Testing Your Model
So far, we used the trainingRDD and validationRDD datasets to select the best model. Since we used these two datasets to determine what model is best, we cannot use them to test how good the model is - otherwise we would be very vulnerable to overfitting. To decide how good our model is, we need to use the testRDD dataset. We will use the bestRank you determined in part (2c) to create a model for predicting the ratings for the test dataset and then we will compute the RMSE.
The steps you should perform are:
- Train a model, using the
trainingRDD,bestRankfrom part (2c), and the parameters you used in in part (2c):seed=seed,iterations=iterations, andlambda_=regularizationParameter- make sure you include all of the parameters. - For the prediction step, create an input RDD,
testForPredictingRDD, consisting of (UserID, MovieID) pairs that you extract fromtestRDD. You will end up with an RDD of the form:[(1, 1287), (1, 594), (1, 1270)] - Use myModel.predictAll() to predict rating values for the test dataset.
- For validation, use the
testRDDand yourcomputeErrorfunction to compute the RMSE betweentestRDDand thepredictedTestRDDfrom the model. - Evaluate the quality of the model by using the
computeError()function you wrote in part (2b) to compute the error between the predicted ratings and the actual ratings intestRDD.
(2e) Comparing Your Model
Looking at the RMSE for the results predicted by the model versus the values in the test set is one way to evalute the quality of our model. Another way to evaluate the model is to evaluate the error from a test set where every rating is the average rating for the training set.
The steps you should perform are:
- Use the
trainingRDDto compute the average rating across all movies in that training dataset. - Use the average rating that you just determined and the
testRDDto create an RDD with entries of the form (userID, movieID, average rating). - Use your
computeErrorfunction to compute the RMSE between thetestRDDvalidation RDD that you just created and thetestForAvgRDD.
Part 3: Predictions for Yourself
The ultimate goal of this lab exercise is to predict what movies to recommend to yourself. In order to do that, you will first need to add ratings for yourself to the ratingsRDD dataset.
(3a) Your Movie Ratings
To help you provide ratings for yourself, we have included the following code to list the names and movie IDs of the 100 highest-rated movies from movieLimitedAndSortedByRatingRDD which we created in part 1 the lab.
print 'Most rated movies:'
print '(average rating, movie name, number of reviews)'
for ratingsTuple in movieLimitedAndSortedByRatingRDD.take(100):
print ratingsTuple
Most rated movies:
(average rating, movie name, number of reviews)
(4.5349264705882355, u'Shawshank Redemption, The (1994)', 1088)
(4.515798462852263, u"Schindler's List (1993)", 1171)
(4.512893982808023, u'Godfather, The (1972)', 1047)
(4.510460251046025, u'Raiders of the Lost Ark (1981)', 1195)
(4.505415162454874, u'Usual Suspects, The (1995)', 831)
(4.457256461232604, u'Rear Window (1954)', 503)
(4.45468509984639, u'Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb (1963)', 651)
(4.43953006219765, u'Star Wars: Episode IV - A New Hope (1977)', 1447)
(4.4, u'Sixth Sense, The (1999)', 1110)
(4.394285714285714, u'North by Northwest (1959)', 700)
(4.379506641366224, u'Citizen Kane (1941)', 527)
(4.375, u'Casablanca (1942)', 776)
(4.363975155279503, u'Godfather: Part II, The (1974)', 805)
(4.358816276202219, u"One Flew Over the Cuckoo's Nest (1975)", 811)
(4.358173076923077, u'Silence of the Lambs, The (1991)', 1248)
(4.335826477187734, u'Saving Private Ryan (1998)', 1337)
(4.326241134751773, u'Chinatown (1974)', 564)
(4.325383304940375, u'Life Is Beautiful (La Vita \ufffd bella) (1997)', 587)
(4.324110671936759, u'Monty Python and the Holy Grail (1974)', 759)
(4.3096, u'Matrix, The (1999)', 1250)
(4.309457579972183, u'Star Wars: Episode V - The Empire Strikes Back (1980)', 1438)
(4.30379746835443, u'Young Frankenstein (1974)', 553)
(4.301346801346801, u'Psycho (1960)', 594)
(4.296438883541867, u'Pulp Fiction (1994)', 1039)
(4.286535303776683, u'Fargo (1996)', 1218)
(4.282367447595561, u'GoodFellas (1990)', 811)
(4.27943661971831, u'American Beauty (1999)', 1775)
(4.268053855569155, u'Wizard of Oz, The (1939)', 817)
(4.267774699907664, u'Princess Bride, The (1987)', 1083)
(4.253333333333333, u'Graduate, The (1967)', 600)
(4.236263736263736, u'Run Lola Run (Lola rennt) (1998)', 546)
(4.233807266982622, u'Amadeus (1984)', 633)
(4.232558139534884, u'Toy Story 2 (1999)', 860)
(4.232558139534884, u'This Is Spinal Tap (1984)', 516)
(4.228494623655914, u'Almost Famous (2000)', 744)
(4.2250755287009065, u'Christmas Story, A (1983)', 662)
(4.216757741347905, u'Glory (1989)', 549)
(4.213358070500927, u'Apocalypse Now (1979)', 539)
(4.20992028343667, u'L.A. Confidential (1997)', 1129)
(4.204733727810651, u'Blade Runner (1982)', 845)
(4.1886120996441285, u'Sling Blade (1996)', 562)
(4.184615384615385, u'Braveheart (1995)', 1300)
(4.184168012924071, u'Butch Cassidy and the Sundance Kid (1969)', 619)
(4.182509505703422, u'Good Will Hunting (1997)', 789)
(4.166969147005445, u'Taxi Driver (1976)', 551)
(4.162767039674466, u'Terminator, The (1984)', 983)
(4.157545605306799, u'Reservoir Dogs (1992)', 603)
(4.153333333333333, u'Jaws (1975)', 750)
(4.149840595111583, u'Alien (1979)', 941)
(4.145015105740181, u'Toy Story (1995)', 993)
(4.142857142857143, u'M*A*S*H (1970)', 518)
(4.129737609329446, u"Ferris Bueller's Day Off (1986)", 686)
(4.124678663239075, u'Die Hard (1988)', 778)
(4.122596153846154, u'Aliens (1986)', 832)
(4.121270452358036, u'Forrest Gump (1994)', 1039)
(4.11251580278129, u'Indiana Jones and the Last Crusade (1989)', 791)
(4.111470113085622, u'Annie Hall (1977)', 619)
(4.107407407407408, u'Green Mile, The (1999)', 540)
(4.092905405405405, u'Shakespeare in Love (1998)', 1184)
(4.090289608177172, u'Full Metal Jacket (1987)', 587)
(4.083788706739527, u'Being John Malkovich (1999)', 1098)
(4.084126984126984, u'Apollo 13 (1995)', 630)
(4.081309398099261, u'Stand by Me (1986)', 947)
(4.075182481751825, u'Terminator 2: Judgment Day (1991)', 1370)
(4.075043630017452, u'Clockwork Orange, A (1971)', 573)
(4.07521578298397, u'2001: A Space Odyssey (1968)', 811)
(4.072258064516129, u'Hunt for Red October, The (1990)', 775)
(4.071129707112971, u'Fugitive, The (1993)', 956)
(4.068078668683812, u'Rain Man (1988)', 661)
(4.057971014492754, u'Platoon (1986)', 552)
(4.053763440860215, u'Gone with the Wind (1939)', 558)
(4.051724137931035, u'When Harry Met Sally... (1989)', 754)
(4.050151975683891, u'Raising Arizona (1987)', 658)
(4.049358341559723, u'Gladiator (2000)', 1013)
(4.042488619119879, u'Close Encounters of the Third Kind (1977)', 659)
(4.040998217468806, u'Animal House (1978)', 561)
(4.039285714285715, u'Seven (Se7en) (1995)', 560)
(4.037406483790524, u'Back to the Future (1985)', 1203)
(4.0356472795497185, u'Blazing Saddles (1974)', 533)
(4.035251798561151, u'Star Wars: Episode VI - Return of the Jedi (1983)', 1390)
(4.02020202020202, u'Fight Club (1999)', 693)
(3.998019801980198, u'American Graffiti (1973)', 505)
(3.989833641404806, u'E.T. the Extra-Terrestrial (1982)', 1082)
(3.9784560143626573, u'Groundhog Day (1993)', 1114)
(3.969639468690702, u'Rocky (1976)', 527)
(3.9686924493554327, u'Untouchables, The (1987)', 543)
(3.9612724757952975, u'As Good As It Gets (1997)', 723)
(3.9591503267973858, u'Fish Called Wanda, A (1988)', 612)
(3.9549929676511955, u'Clerks (1994)', 711)
(3.9509703779366703, u'Airplane! (1980)', 979)
(3.949814126394052, u'Beauty and the Beast (1991)', 538)
(3.925512104283054, u'Few Good Men, A (1992)', 537)
(3.924882629107981, u'Babe (1995)', 852)
(3.921985815602837, u'Twelve Monkeys (1995)', 705)
(3.9189704480457577, u'Ghostbusters (1984)', 1049)
(3.9176904176904177, u'Election (1999)', 814)
(3.916445623342175, u'Chicken Run (2000)', 754)
(3.9130434782608696, u'Dances with Wolves (1990)', 690)
(3.907275320970043, u"There's Something About Mary (1998)", 701)
(3.894977168949772, u'Star Trek: The Wrath of Khan (1982)', 657)
The user ID 0 is unassigned, so we will use it for your ratings. We set the variable myUserID to 0 for you. Next, create a new RDD myRatingsRDD with your ratings for at least 10 movie ratings. Each entry should be formatted as (myUserID, movieID, rating) (i.e., each entry should be formatted in the same way as trainingRDD). As in the original dataset, ratings should be between 1 and 5 (inclusive). If you have not seen at least 10 of these movies, you can increase the parameter passed to take() in the above cell until there are 10 movies that you have seen (or you can also guess what your rating would be for movies you have not seen).
myUserID = 0
# Note that the movie IDs are the *last* number on each line. A common error was to use the number of ratings as the movie ID.
myRatedMovies = [
(myUserID, 1110, 5),
(myUserID, 1088, 5),
(myUserID, 1337, 4),
(myUserID, 1447, 3),
(myUserID, 744, 4),
(myUserID, 1248, 5),
(myUserID, 1300, 5),
(myUserID, 832, 4),
(myUserID, 789, 5),
(myUserID, 693, 5)
# The format of each line is (myUserID, movie ID, your rating)
# For example, to give the movie "Star Wars: Episode IV - A New Hope (1977)" a five rating, you would add the following line:
# (myUserID, 260, 5),
]
myRatingsRDD = sc.parallelize(myRatedMovies)
(3b) Add Your Movies to Training Dataset
Now that you have ratings for yourself, you need to add your ratings to the training dataset so that the model you train will incorporate your preferences. Spark’s union() transformation combines two RDDs; use union() to create a new training dataset that includes your ratings and the data in the original training dataset.
(3c) Train a Model with Your Ratings
Now, train a model with your ratings added and the parameters you used in in part (2c): bestRank, seed=seed, iterations=iterations, and lambda_=regularizationParameter - make sure you include all of the parameters.
(3d) Check RMSE for the New Model with Your Ratings
Compute the RMSE for this new model on the test set.
- For the prediction step, we reuse
testForPredictingRDD, consisting of (UserID, MovieID) pairs that you extracted fromtestRDD. The RDD has the form:[(1, 1287), (1, 594), (1, 1270)] - Use
myRatingsModel.predictAll()to predict rating values for thetestForPredictingRDDtest dataset, set this aspredictedTestMyRatingsRDD - For validation, use the
testRDDand yourcomputeErrorfunction to compute the RMSE betweentestRDDand thepredictedTestMyRatingsRDDfrom the model.
(3e) Predict Your Ratings
So far, we have only used the predictAll method to compute the error of the model. Here, use the predictAll to predict what ratings you would give to the movies that you did not already provide ratings for.
The steps you should perform are:
- Use the Python list
myRatedMoviesto transform themoviesRDDinto an RDD with entries that are pairs of the form (myUserID, Movie ID) and that does not contain any movies that you have rated. This transformation will yield an RDD of the form:[(0, 1), (0, 2), (0, 3), (0, 4)]. Note that you can do this step with one RDD transformation. - For the prediction step, use the input RDD,
myUnratedMoviesRDD, with myRatingsModel.predictAll() to predict your ratings for the movies.
(3f) Predict Your Ratings
We have our predicted ratings. Now we can print out the 25 movies with the highest predicted ratings.
The steps you should perform are:
- From Parts (1b) and (1c), we know that we should look at movies with a reasonable number of reviews (e.g., more than 75 reviews). You can experiment with a lower threshold, but fewer ratings for a movie may yield higher prediction errors. Transform
movieIDsWithAvgRatingsRDDfrom Part (1b), which has the form (MovieID, (number of ratings, average rating)), into an RDD of the form (MovieID, number of ratings):[(2, 332), (4, 71), (6, 442)] - We want to see movie names, instead of movie IDs. Transform
predictedRatingsRDDinto an RDD with entries that are pairs of the form (Movie ID, Predicted Rating):[(3456, -0.5501005376936687), (1080, 1.5885892024487962), (320, -3.7952255522487865)] - Use RDD transformations with
predictedRDDandmovieCountsRDDto yield an RDD with tuples of the form (Movie ID, (Predicted Rating, number of ratings)):[(2050, (0.6694097486155939, 44)), (10, (5.29762541533513, 418)), (2060, (0.5055259373841172, 97))] - Use RDD transformations with
predictedWithCountsRDDandmoviesRDDto yield an RDD with tuples of the form (Predicted Rating, Movie Name, number of ratings), for movies with more than 75 ratings. For example:[(7.983121900375243, u'Under Siege (1992)'), (7.9769201864261285, u'Fifth Element, The (1997)')]